

Autor: Bodoconsult EDV-Dienstleistungen GmbH, Robert Leisner
Wir wollen Ihnen nun wirklich wichtigen mathematischen Grundlagen und Begriffe für die private Finanzplanung zeigen. Unser Motto dabei ist: so einfach wie möglich, so kompliziert wie nötig! Konzetrieren wir uns aus das Wesentliche!

Die Rendite ist eine der wichtigsten Entscheidungsgrundlagen bei der Auswahl von Geldanlagen. Der Begriff Rendite kann (und wird) jedoch sehr unterschiedlich definiert, womit Renditezahlen nur sehr bedingt miteinander vergleichbar sind.
Verschiedene Arten von Geldanlagen unterscheiden sich teilweise sehr stark in der Kapitalbindung. Je höher die Kapitalbindung ist, desto wichtiger wird die Berücksichtigung der Zeitgewichtung der Zahlungsströme. Geldanlagen, bei denen man z.B. sehr schnell das eingesetzte Kapital zurückerhält, jedoch über eine deutlich längere Zeit Erträge erzielt, können z.B. nur über die Berechnung des Internen Zinsfußes sinnvoll bewertet werden.
Die Rendite berechnet als Interner Zinsfuß lässt sich aber z.B. nicht mit der einfachen Rendite einer festverzinslichen Anleihe vergleichen. Aus diesem Grund sind Vergleiche von Renditen mit großer Vorsicht zu betrachten. Unter Umständen werden sonst Äpfel mit Birnen verglichen.
Die einfache Rendite gibt an, um wie viel Prozent das Endvermögen gegenüber dem Startvermögen gewachsen ist. Dabei spielt die Zeitdauer zwischen beiden Zeitpunkten keine Rolle. Das kann zu zweifelhaften Interpretation führen: Eine einfache Rendite von 50% wird sicher interessanter sein, wenn sie in zwei Jahren erzielt wurde, als in 10 Jahren.
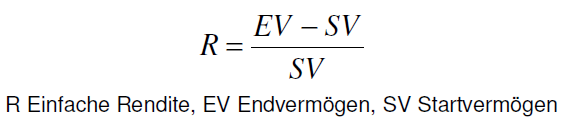
Beispiel: Das Startvermögen SV beträgt 100, das Endvermögen EV 120. Damit ergibt sich eine einfache Rendite von 20%.
Die durchschnittliche Rendite ergibt sich aus der einfachen Rendite, in dem man diese durch die Anlagedauer teilt. Damit berücksichtigt die durchschnittliche Rendite nicht den Zinseszinseffekt, was vor allem bei längeren Laufzeiten einen gravierenden Mangel bedeutet.
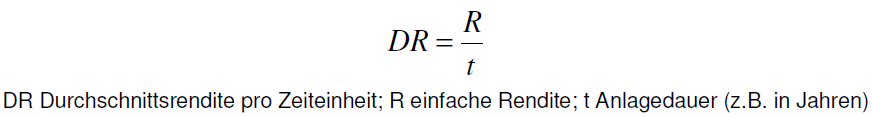
Beispiel: Die einfache Rendite von 20% wurde über einen Zeitraum von fünf Jahren erzielt. Damit ergibt sich eine durchschnittliche Rendite von 4%.
Die zeitgewichtete Rendite ergibt sich als Zinssatz einer einmaligen festverzinslichen Anleihe SV, die unter Berücksichtigung des Zinseszinseffekts das gleiche Ergebnis EY liefert. Dabei wird nicht berücksichtigt, dass in der Praxis möglicherweise zu verschiedenen Zeitpunkten in eine Geldanlage investiert wird. Damit wird die unterschiedliche Kapitalbindung nicht berücksichtigt. Letztlich wird so getan, also ob eine Einmalanlage zu einem bestimmten Zinssatz erfolgt.

Beispiel: 20% einfache Rendite in fünf Jahren bedeuten eine zeitgewichtete Rendite von 3,71%.
Der Interne Zinsfuß oder englisch internal rate of return (IRR) ist ein Renditemaß, das unterschiedliche Zeiträume zwischen Zahlungszeitpunkten berücksichtigt. Die oben genannten Renditemaße können unterschiedliche Zahlungszeiträume nicht berücksichtigen.
Die Berechnung des Internen Zinsfußes erfolgt über einen komplizierten mathematischen Algorithmus, der auch mehrdeutige Ergebnisse liefern kann. Theoretisch ist der Interne Zinsfuß eines der besten Renditemaße, da die zeitlich veränderliche Kapitalbindung berücksichtigt wird.
Voraussetzung für die Gültigkeit des Internen Zinsfußes ist die Annahme, dass Erträge mit dem gleichen internen Zinsfuß wieder angelegt werden. Diese Annahme dürfte in der Praxis oft nur schwer umsetzbar sein. Damit gibt der Interne Zinsfuß aus Sicht des Anlegers regelmäßig eine zu hohe Rendite an.
Typische Geldanlagen, die über den Internen Zinsfuß beurteilt werden, sind nicht börsennotierte Unternehmensbeteiligungen oder geschlossene Fonds.
Der Interne Zinsfuß kann z.B. in Excel mit Hilfe der Funktion IKV aus einer Zahlungsreihe berechnet werden.
Weitere Informationen zur IRR unter https://de.wikipedia.org/wiki/Interner_Zinsfu%C3%9F.
Risiko wird heute in der Finanzwelt definiert als die (absolute) Schwankungsbreite der Rendite um ihren Erwartungswert. Die Schwankungen der realen Renditen können positiv als Chance oder negativ als Risiko betrachtet werden. Man bezeichnet das Risiko auch mit dem Begriff Volatilität.
Mathematisch gesehen wird das Risiko als Standardabweichung σ der realen stetigen Renditen gemessen. Die stetigen Renditen sind logarithmierte Renditen für einen unendlichen kleinen Zeitraum, was aber für das grundsätzliche Verständnis des folgenden keine wesentliche Rolle spielt. Als Erwartungswert der Rendite wird normalerweise der historische Durchschnittswert μ der stetigen Rendite in einem gewissen Zeitraum gewählt.
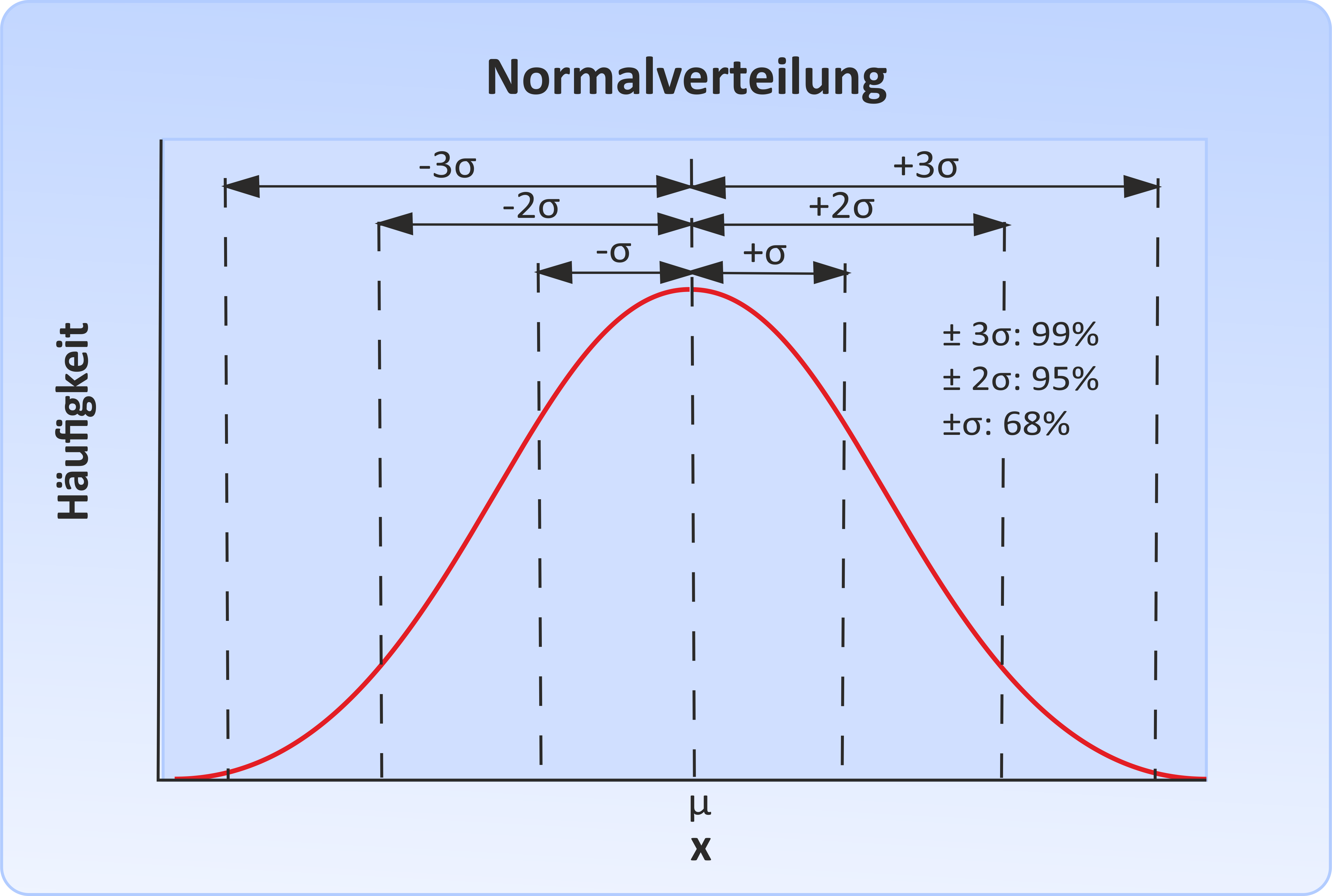
Mit diesen Annahmen ergibt sich für die Verteilung der Renditen eine Normalverteilung. Im folgenden Diagramm ist die Rendite auf der x-Achse angetragen. Auf der y-Achse ist die Häufigkeit der jeweiligen Rendite angetragen. Es ergibt sich die klassische Glockenkurve der Normalverteilung:
Im Gegensatz zur Ungewissheit verfügt man bei Unsicherheit (=Risiko) über die Wahrscheinlichkeiten des Auftretens von gewissen Ereignissen. Nicht nur zu wissen, was alles passieren kann, sondern auch wie oft etwas passiert, ist ein wesentlicher Vorteil. Damit lassen sich Kosten und Nutzen von Sicherungsmaßnahmen abschätzen. Und genau das macht man letztlich bei der Geldanlage: Chancen und Risiken abwägen.
Das Risiko wird in Prozent angegeben. Beträgt die historische Durchschnittsrendite z.B. 5% pro Jahr und die Volatilität (das Risiko) 10%, so werden die realen erwarteten Renditen mit 68% Wahrscheinlichkeit zwischen +15% und -5% pro Jahr liegen. Da es sich um Wahrscheinlichkeitsbetrachtungen handelt, können auch Renditen außerhalb dieses Bereichs auftreten. Man spricht dann im negativen Fall von einem Crash.
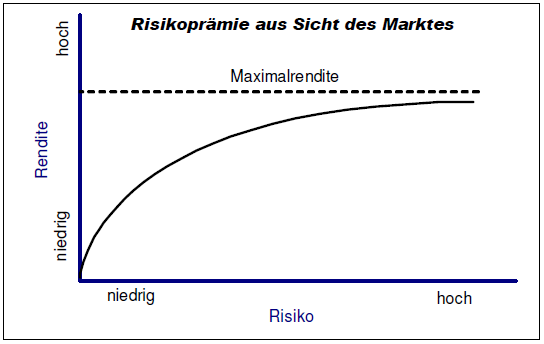
Zwischen Risiko und Rendite besteht ein grundsätzlicher Zusammenhang: Für eine höhere Rendite muß man ein höheres Risiko eingehen. Den Mehrertrag, den man bei einem höheren Risiko gegenüber einer risikolosen Geldanlage erzielt, bezeichnet man als Risikoprämie.
Aus Sicht des Investors muss ein höheres Risiko mit einer zunehmend steigenden Risikoprämie belohnt werden:
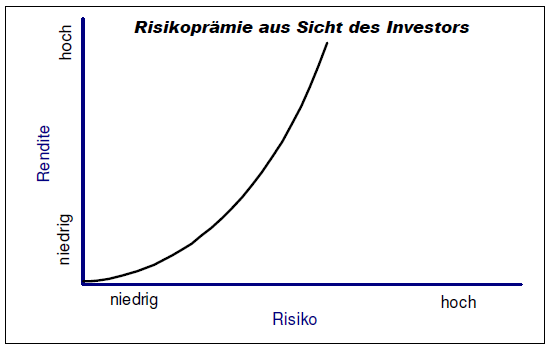
Würde der Markt entsprechend den Wünschen der Investoren ein steigendes Risiko mit einer stärker steigenden Risikoprämie belohnen, so würde dies zu extremen Spekulationen aller Marktteilnehmer führen. Das übernommene Risiko würde ungesund ansteigen bis zum Crash. Daher vergütet der Markt ein höheres Risiko zwar schon mit einer höheren Rendite, jedoch nehmen die Zuwächse der Rendite ab und nähern sich einer maximal erzielbaren Rendite an.
Diesen Effekt bezeichnet man als das Prinzip des abnehmenden Grenznutzen.
Einer der wichtigsten Einflussfaktoren für den erfolgreichen Vermögensaufbau ist die Inflation. Als Inflation bezeichnet man einen Preisanstieg auf breiter Front. Inflation gibt letztlich an, wieviel weniger Ihr Geld in der Zukunft wert ist. Eine Inflationsrate von 3% bedeutet, dass Ihr Geld jedes Jahr um 3% weniger Wert ist. Die reale Kaufkraft des Geldes sinkt, nominal bleibt alles unverändert.
Vermögensaufbau kann auf zwei Wegen erfolgen: durch Zuführung neuer Gelder ins Vermögen und durch Erzielung einer Rendite auf das vorhandene Vermögen. Der zweite Weg der Renditeerzielung macht sich den Zinseszinseffekt zunutze. Leider hat die Inflation aber gerade auf den Zinseszinseffekt einen entscheidenden Einfluß. Ist nämlich die erzielte Rendite kleiner als die Inflationsrate, so erzielt man zwar nominal einen Vermögenszuwachs, real aber verliert das Vermögen an Wert. Daher müssen Sie mindestens eine Rendite nach Kosten und Steuern in Höhe der Inflationsrate erzielen, um wenigstens keinen (realen) Vermögensverlust zu haben.
Der nominale Geldwert ist einfach der zahlenmäßige Betrag des Geldes an einem bestimmten Zeitpunkt. Besitzt man heute 100.000 EUR, so ist der nominale Geldwert heute auch 100.000 EUR. Hat man die 100.000 EUR erst in fünf Jahren, so beträgt der nominale Geldwert in fünf Jahren ebenfalls 100.000 EUR.
Der reale Geldwert ist immer in Bezug auf einen anderen Zeitpunkt zu sehen. Die 100.000 EUR in fünf Jahren im obigen Beispiel sind real, also nach Berücksichtigung der Inflation, im Vergleich zu heute viel weniger wert. Reale Geldwerte berücksichtigen also die tatsächliche oder erwartete Inflation zwischen zwei Zeitpunkten.
Der Barwert von Geld ist der heutige Wert einer in der Zukunft erfolgenden Zahlung. Herrscht Inflation, so ist eine zukünftige Zahlung stets weniger wert als eine Zahlung gleichen Betrags heute. 10.000 Euro heute zu erhalten ist etwas anderes als 10.000 Euro in 20 Jahren zu erhalten.
Zur Beurteilung von Investitionen ist es nun wichtig, den heutigen Wert – den Barwert – einer zukünftigen Zahlung berechnen („abzinsen“) zu können. Dazu müssen Sie jedoch Annahmen über die zu erwartende Inflation für den Zeitraum bis zur Zahlung treffen. Historisch gesehen ist eine Inflationsrate von 3% ein guter Schätzer.
Die mathematische Formel für die Berechnung des Barwerts lautet:
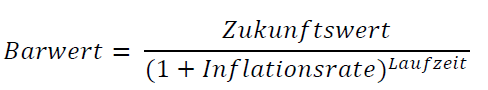
Rechnen Sie beispielsweise mit 3% Inflation, dann ergibt sich der Barwert einer Zahlung von 10.000 EUR in 20 Jahren wie folgt:
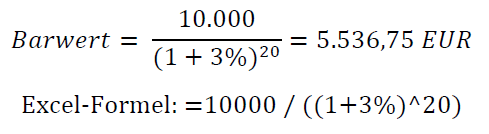
Die Zahlung von 10.000 EUR in 20 Jahren ist also in heutiger Kaufkraft nur 5.536,75 EUR wert.
Der Zinseszinseffekt ist die größte mathematische Entdeckung aller Zeiten.
Albert Einstein
Die mathematische Formel für den Zinseszinseffekt einer Einmalanlage lautet:
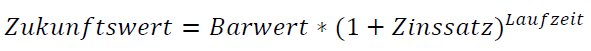
Legen Sie heute 10.000 EUR zu 5% p.a. für 20 Jahre an, ergibt sich:
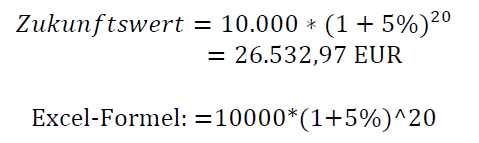
Nach 20 Jahren erhalten sie also 26.532,97 EUR ausgezahlt. Der Barwert eines Zukunftswerts von 26.532,97 EUR bei 3% Inflation beträgt 14,590,85 EUR. Damit erwirtschaftet die heutige Geldanlage von 10.000 EUR bei 5% in 20 Jahren einen Vermögenszuwachs von 4.590,85 EUR in heutiger Kaufkraft.
Wieder angelegte Zinsen erwirtschaften wiederum Zinsen. Dieser enorm wichtige Effekt wird regelmäßig unterschätzt. Die folgende Tabelle in nominalen Geldwerten verdeutlicht dies. Dabei zeigen die roten Spalten die Entwicklung bei Renditen unter der Inflationsrate, d.h. bei einem realen Kaufkraftverlust. Die blaue Spalte zeigt gerade die Erhaltung der Kaufkraft. Bei den schwarzen Spalten nimmt die reale Kaufkraft zu.
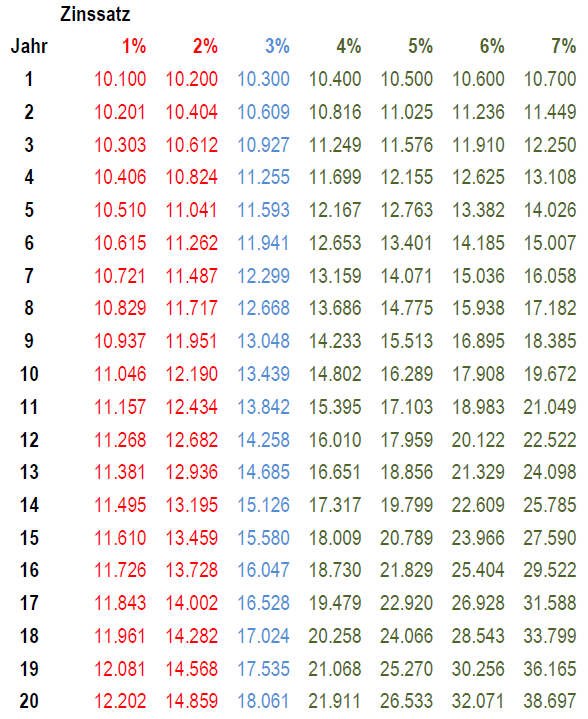
Als Anleger braucht man Zeit und Geduld, um den Zinseszinseffekt nutzen zu können. Besitzt man beides, wird man ohne weitere eigene Anstrengungen reich belohnt. Außerdem sieht man in der obigen Tabelle schön die Bedeutung einer höheren Verzinsung. Eine höhere Verzinsung kann man oft bei gleichbleibendem Risiko allein durch niedrigere Kosten erzielen.
Hinweis: Eine Verzinsung von 3% entspricht in etwa der Inflationsrate, d.h. Sie erzielen damit gerade einmal den realen Erhalt des Geldwerts.
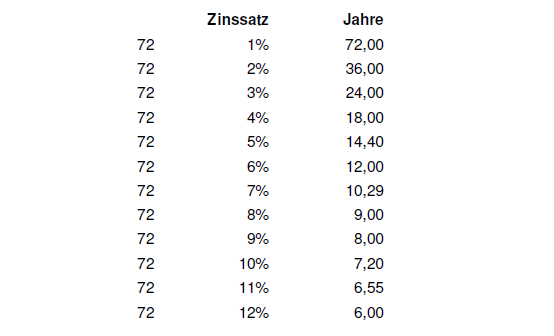
Hinweis: Zur schnellen Beurteilung des Zinseszinseffekts kann die 72er-Regel verwendet werden: Teilen Sie 72 durch den Zinssatz (Inflationsrate) und Sie wissen, wann sich der Geldwert verdoppelt (halbiert) hat.
Viele Geldanleger wollen regelmäßig Geld anlegen, häufig in Aktienfonds. Hier stellt sich die Frage, was günstiger ist: regelmäßig eine gleiche Stückzahl eines Fonds zu kaufen oder lieber regelmäßig einen festen Betrag anzulegen.
In jeden von drei verschiedenen Fonds - A, B und C - werden monatlich 100 Euro eingezahlt. Der Sparplan dauert ein Jahr. Die Tabelle zeigt die Kurse jeweils zu Monatsbeginn.

Zinst man alle Zahlungsströme einer geplanten Investition auf den heutigen Tag ab, d.h. berechnet man den Barwert aller heutigen bzw. zukünftigen Zahlungen, und summiert die Barwerte auf, erhält man den Barwert der Investition. Ist dieser größer als Null, so ist die Investition grundsätzlich sinnvoll, wobei über die erzielte Rendite noch nichts gesagt ist.
Vor allem bei sehr langfristigen Investitionen, z.B. im Privatbereich eine Photovoltaikanlage, sollten Sie den Kapitalwert berechnen, da Sie sonst u.U. finanziell völlig unsinnige Investitionen tätigen werden.
Auch bei der Beurteilung einer Immobilie als selbstbewohnte oder vermietete Geldanlage ist der Kapitalwert eine sehr wichtige Beurteilungsgröße: Eine Immobilie wird heute für 100.000 EUR gekauft, der Verkaufspreis in 20 Jahren wird mit 170.000 EUR angenommen bei 3% Inflation. Die ersparte Miete entspricht den Kreditzahlungen. Der Barwert des Verkaufspreises beträgt 94.124,87 EUR. Der Kapitalwert der Immobilien beträgt -100.000 + 94.124,87 = -5.875,12 EUR. Damit verliert man in diesem Fall real Vermögen!
| Funktion | Bemerkung |
|---|---|
| BW() | Barwertberechnung für regelmäßige Zahlungen ermitteln |
| ZW() | Zukunftswertberechnung für regelmäßige Zahlungen ermitteln |
| RMZ() | Berechnung der Annuität eines Darlehens |
| IKV() | Internen Zinsfuß berechnen für eine Reihe an Zahlungen |